通过 Lisp 语言理解编程算法：数据结构篇

此前，InfoQ 已经翻译并分享了本系列的前两章：《简介和复杂度》、《 Lisp 速成课程》，现在，我们即将介绍数据结构。数据结构（data structure）是计算机中存储、组织数据的方式。数据结构意味着接口或封装：一个数据结构可被视为两个函数之间的接口，或者是由数据类型联合组成的存储内容的访问方法封装。在本章中，我们将阐述 Lisp 中的数据结构。

在接下来的几章中，我们将描述每种编程语言提供的基本数据结构、它们的用法以及与之相关的最重要算法。我们将从数据结构和元组或结构的概念开始，它们是最原始、最基本的概念。

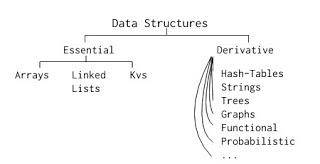
数据结构与算法

让我们从一个有点抽象的问题开始：算法和数据结构，哪个更重要？

从一个角度来看，算法是许多程序的本质，而数据结构似乎是次要的。此外，尽管大多数算法依赖于特定数据结构的某些特性，但并非所有算法都依赖这些特性。数据结构依赖算法的好例子是堆排序（Heapsort）、使用二叉查找树（Binary Search Tree，BST）搜索、并查集（union-find）。而第二种是：Erastophenes 筛选法（埃拉托色尼筛选法，简称艾氏筛法）和一致哈希（consistent hashing）。

译注：

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

二叉查找树（Binary Search Tree），也称二叉搜索树、有序二叉树（ordered binary tree），排序二叉树（sorted binary tree）。二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低。为 O(log n)。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、multiset、关联数组等。

并查集，计算机科学中，并查集是一种树型的数据结构，其保持着用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。

埃拉托色尼筛选法 （sieve of Erastophenes），也称素数筛。这是一种简单且历史悠久的筛法，用来找出一定范围内所有的素数。它是列出所有小素数最有效的方法之一，其名字来自于古希腊数学家埃拉托斯特尼（Erastophenes），并且被描述在另一位古希腊数学家尼科马库斯（Nicomachus）所著的《算术入门》（Introduction to Arithmetic）中。

一致哈希 （consistent hashing）, 由 MIT 的 Karger 及其合作者提出，现在这一思想已经扩展到其它领域。在这篇 1997 年发表的学术论文中介绍了 “一致哈希” 如何应用于用户易变的分布式 Web 服务中。哈希表中的每一个代表分布式系统中一个节点，在系统添加或删除节点只需要移动 K/n 项。一致哈希的概念还被应用于分布式散列表（DHT）的设计。DHT 使用一致哈希来划分分布式系统的节点。所有关键字都可以通过一个连接所有节点的覆盖网络高效地定位到某个节点。

与此同时，一些经验丰富的开发人员指出，当找到正确的数据结构时，算法几乎会“自动”地编写出来。Linux 之父 Linus Torvalds 曾经表示：

烂程序员关心的是代码。好程序员关心的是数据结构和它们之间的关系。（Bad programmers worry about the code. Good programmers worry about data structures and their relationships.）

Eric S. Raymond 在《UNIX 编程艺术》（Art of Unix Programming）一书中，对同一个想法提出了不那么尖锐的版本，称之为“表示原则”（Rule of Representation）：

把知识叠入数据以求逻辑质朴而健壮。

即时最简单的程序逻辑让人类来验证也很困难，但是就算是很复杂的数据，对人类来说，还是相对容易地就能够推导和建模的。不信可以试试比较一下，是五十个节点的指针树，还是五十行代码的流程图更清楚明了；或者，比较一下究竟用一个数组初始化器来表示转换表，还是用 switch 语句更清楚明了呢？可以看出，不同的方式在透明性和清晰性方面具有非常显著的差别。

数据要比编程逻辑更容易驾驭。所以接下来，如果要在复杂数据和复杂代码中选择一个，宁愿选择前者。更进一步，在设计中，你应该主动将代码的复杂性转移到数据之中去。

数据结构比算法更为静态。当然，它们中的大多数都允许随着时间的推移而改变它们的内容，但是总有某些不变量存在。这允许通过简单的归纳进行推理：只考虑两种（或至少少数），即基本情况和一般情况。换句话说，数据架构基本上不再考虑时间的概念，并且随着时间而变化是导致程序复杂性的主要原因之一。也就是说，数据结构是声明性的，而大多数算法是命令式的。声明性方法的优点是，你无需想象（追踪）随时间流动会发生什么样的变化。

因此，本书像大多数关于该主题的其他书籍一样，也是围绕数据结构组织的。大多数章节介绍了一个特定的结构、属性和接口，并解释了与之相关的算法，展示了它的实际用例。然而，一些重要的算法并不需要特定的数据结构，因此，也有几个章节专门对它们进行讨论。

数据结构概念

在数据结构中，实际上有两种不同的类型：抽象和具体。它们之间的显著区别在于，抽象结构只是一个接口（一组操作）和一些必须满足的条件或不变量。它们的特定实现由具体的数据结构提供，这些实现可能在效率特性和内部机制方面存在显著的差异。例如，抽象数据结构队列（queue）只有两个操作： enqueue 将项目添加到队列的末尾，dequeue 在开头获取一个项目并将其从队列中删除。还有一个约束条件，即项目应该按照它们入列的相同顺序出列。现在，队列可以使用许多不同的底层数据结构来实现：链表或双链表、数组或树。每一个都具有不同的效率特性和队列接口之外的附加属性。我们将在书中讨论这两种类型，重点放在具体结构上，并解释它们在实现特定抽象接口时的用法。

近年来，“数据结构”这一术语，已经有些失宠了，在面向对象的函数式编程范例或类的上下文中，通常被概念上更为丰富的类型概念所取代。然而，对于本书来说，这两个概念都不仅仅意味着我们只关心算法机制。首先，在算法的上下文中，它们还区分了所有无显著差异的原始值（数字、字符等）。此外，类形成继承的层次结构，而类型与范畴论（category theory）的代数规则相关联。因此，在本书中，我们将解释使用中性的数据结构术语，并在适当情况下偶尔提及其他变体。

译注： 范畴论（category theory），是数学的一门学科，以抽象的方法来处理数学概念，将这些概念形式化成一组组的“对象”及“态射”。范畴最容易理解的一个例子为集合范畴，其对象为集合，态射为集合间的函数。但需注意，范畴的对象不一定要是集合，态射也不一定要是函数；一个数学概念若可以找到一种方法，以符合对象及态射的定义，则可形成一个有效的范畴，且所有在范畴论中导出的结论都可应用在这个数学概念之上。

相连数据结构与链接数据结构

当前的计算机体系结构由中央处理器（CPU）、存储器和外围输入输出设备组成。数据通过 I/O 设备，存储在内存中，由 CPU 进行处理，以某种方式与外界进行交换。还有一个关键的约束因素，称为冯诺依曼瓶颈：即 CPU 只能处理存储在有限数量的特殊基本内存块（称为寄存器）中的数据。因此，它必须不断地在寄存器和主存储器之间来回移动数据元素（使用中间缓存来加快该过程）。现在，有些东西可以放入寄存器，有些则不能。第一个被称为原语（primitive），主要是将那些可以直接用整数表示的项联合起来：整数 、浮点数、字符。所有需要自定义数据结构来表示的所有内容都不能作为一个整体放入寄存器中。

另一个适用于处理器寄存器的项目是内存地址。实际上，有一个重要的常量：通用寄存器中的位数，它定义了特定 CPU 可以处理的最大内存地址，从而定义了它可以处理的最大内存量。对 32 位架构来说，它是 2^32（4GB）；对于 64 位架构来说，你已经猜到了，它是 2^64。内存地址通常称为指针（pointer），如果你将指针存放在寄存器中，那么有一些命令允许 CPU 从它指向的位置检索内存中的数据。

因此，有两种方法可以将数据结构放入内存中：

• 相连（contiguous）结构占用单个内存块，其内容存储在相邻的内存块中。要访问特定的块，我们应该知道它从分配给该结构的内存范围开始的偏移量。（这通常由编译器处理）。当处理器需要读写这一块时，它将使用指针，该指针作为结构的基址和偏移量之和来计算。相连结构的例子是数组和结构。

• 相反，链接结构不占用相连的内存块，即其内容位于不同的位置。这意味着只想特定块的指针不能预先计算，应该存储在结构本身中。这种结构更加灵活，但在访问某个元素所用的空间和时间方面都会增加额外的开销（当有嵌套时，可能需要多个跃点，而在相连结构中，它始终是常量）。存在大量链接数据结构，如列表、树和图。

元组

在大多数语言中，一些常见的数据结构（如数组或列表）是“内置”的，但是，如果我们追根究底的话，就会发现，它们的工作方式大多与任何用户定义的数据结构基本相同。为了实现任意的数据结构，这些语言提供了一种称为记录、结构、对象等的特殊机制。它的正确名称应该是“元组”（tuple）。它是由许多字段组成的数据结构，每个字段包含一个原始值（primitive value）、另一个元组或指向任何类型的另一个元组的指针。这样，元组和表示任何结构，包括嵌套结构和递归结构。在类型论的背景下，这种结构被称为“产品类型”（product types）。

元组是一个抽象的数据结构，它唯一的接口是字段访问器函数（field accessor function）：按名称（命名元组）或索引（匿名元组）。它可通过多种方式实现，但最好使用具有常量时间访问的相连变体。然而，在许多语言中，尤其是动态语言中，程序员经常使用列表或动态数组来创建一次性的 Ad-hoc 元组。

译注： Ad-hoc 是拉丁文常用短语中的一个短语。这个短语的意思是“特设的、特定目的的（地）、即席的、临时的、将就的、专案的”。这个短语通常用来形容一些特殊的、不能用于其它方面的的，为一个特定的问题、任务而专门设定的解决方案。

Python 有一个专用的元组数据类型，通常就是为了这个目的，它本质上是一个链接数据结构。下面的 Python 函数将返回一个十进制的元组（用括号编写）和数字 x 的其余部分：

def truncate(x):dec = int(x)rem = x - decreturn (dec, rem)

这是一种简单且效率不高的方法，当字段数量较少且结构的生命周期较短时，这种方法可能会发挥作用。然而，从效率和代码清晰性的角度来看，一个更好的方法是使用预定义的结构。在 Lisp 中，元组被称为 “struct”，由 defstruct 定义，默认情况下，使用相连表示（尽管有一个选项可以使用底层的链表）。下面是一个简单的成对数据结构（simple pair data structure）的定义（在 Lisp 中称为“slot”），它有两个字段： left 和 right。

(defstruct pairleft right)

这个 defstruct 宏，实际上，生成了若干个定义：结构类型的构造函数，被称为 make-pair，并具有 2 个关键字参数：:left 和 :right 以及字段访问器：pair-left 和 pair-right。此外，结构常见的 print-object 方法将适用于我们的新结构，还可以使用 reader-macro （读取宏）从打印表单中恢复它。以下代码展示了它们是如何组合在一起的：

CL-USER> (make-pair :left "foo" :right "bar")#S(PAIR :LEFT "foo" :RIGHT "bar")CL-USER> (pair-right (read-from-string (prin1-to-string *)))"bar"

prin1-to-string 和 read-from-string 是互补的 Lisp 函数，它们允许以计算机可读的形式打印值（如果提供了适当的 print-function（打印函数）），并将其读取回来。理想情况下，良好的 print-representations 对人类和计算机来说都是可读的，对于代码透明度非常重要，不应该被忽视。

有一种方法可以对定义的每个部分自定义。例如，如果我们计划经常使用“成对”（pair），那么我们可以通过指定 (:conc-name nil) 属性来省略 pair- 前缀。下面是 RUTILS 的一个改进的成对定义和它的简化构造函数，我们将在本书中使用它。它使用 :type list 分配来与 destructuring macro （析构宏）集成。

(defstruct (pair (:type list) (:conc-name nil))"A generic pair with left (LT) and right (RT) elements."lt rt)(defun pair (x y)"A shortcut to make a pair of X and Y."(make-pair :lt x :rt y))

在函数调用中传递数据结构

最后一点。将数据结构与函数一起使用有两种方法：要么通过复制是当的内存区域（按值调用（call-by-value））直接传递它们，这种方法通常应用于原始类型（primitive types）；要么传递指针（按引用调用（call-by-reference））。在第一种情况下，被调用函数中原始结构的内容是无法修改的；而在第二种情况下则是可能能够修改的，因此应该考虑不合理更改的风险。处理这类问题的常用方法是调用任何更改之前制作一个副本，尽管有时原始数据结构可能会发生变化，因此不需要复制。显然，引用调用方法更为通用，因为它允许修改和复制，而且由于复制是按需进行的，因此效率更高。这就是为什么在大多数编程语言中，它是处理结构（和对象）的默认方法。然而，在像 C 这样的低级语言中，这两种变体都得到了支持。此外，在 C++ 中，引用传递（pass-by-reference）有两种类型：传递指针并传递实际上所谓的引用，这是指针上的语法糖，它允许使用非指针语法（点而不是箭头）访问参数，并添加了一些限制。但是，不管特定语言的特性如何，总的观点都是一样的。

作用中的结构：并查集

数据结构有不同的形状和风格。在这里，我想提到一个特殊而有趣的例子，在某种程度上，它既是数据结构又是算法。甚至连名称也涉及到了某些操作，而不是静态形式。大多数更高级的数据结构都有这样的一个特征，即它们不仅由形状和排列来定义，还通过一组适用的操作集来定义。并查集（Union-Find）是一组数据结构的算法，可用于有效确定随时间变化的集合中的集合成员。它们可用于查找网络中不相交的部分、检测图中的循环、查找最小生成树等等。这类问题的实例之一就是自动图像分割：将图像的不同部分、汽车与背景、癌细胞与正常细胞相分离。

译注： 并查集（Union-Find），顾名思义就是有 “合并集合” 和 “查找集合中的元素” 两种操作的关于数据结构的一种算法。它主要涉及两种基本操作：合并和查找。这说明，初始时并查集中的元素是不相交的，经过一系列的基本操作 (Union)，最终合并成一个大的集合。而在某次合并之后，有一种合理的需求：某两个元素是否已经处在同一个集合中了？因此就需要 Find 操作。

让我们考虑以下问题：如何确定图中的两点之间是否存在一条路径？假设一个图是一组点（顶点）和这些点中的某些点对之间的边。图中的路径是从源到目的地的一系列点，每一对点都有一条连接它们的边。如果两个点之间存在某条路径，则它们属于同一个分量，否则，则属于两个不相交的分量。

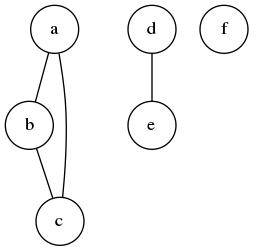
包含三个不想交分量的图。

对于两个任意点，如何确定它们是否存在连接路径？简单的实现可能采用其中一种方法，并开始构建所有可能的路径（这可以以广度优先或深度优先的方式进行，甚至是随机的）。无论如何，这样的过程通常需要一些步骤，与图的顶点数量成正比。我们可以做得更好吗？这是一个常见的问题，它会让我们得到更高效的算法。

并查集方法基于这样一个简单的想法：添加项时，记录它们所属组件的 ID。但如何确定这个 ID 呢？使用与此子集中的某个点关联的 ID，如果该点位于其自身的子集中，则使用当前点的 ID。如果子集已经形成了呢？没问题，我们可以通过迭代每个顶点，并以连接到的任意点的 ID 作为子集的 ID 来模拟添加过程。下面是这种方法的实现（为了简化代码，我们将使用指向 point 结构的指针，而不是 ID，但是，从概念上来说，它们是相同的）：

(defstruct pointparent); if the parent is null the point is the root(defun uf-union (point1 point2)"Join the subsets of POINT1 and POINT2."(:= (point-parent point1) (or (point-parent point2)point2)))(defun uf-find (point)"Determine the id of the subset that a POINT belongs to."(let ((parent (point-parent point)))(if parent(uf-find parent)point)))

只需调用 (make-point) 就会向我们的集合中添加一个包含单个项的新子集。

注意，uf-find 使用递归来查找子集的根，即首先添加的点。因此，对于每个顶点，我们存储一些中间数据，并且为了获得子集 ID，每次我们都要执行额外的计算。这样，我们设法减少了平均情况下的查找时间，但仍然没有完全排除它需要遍历集合中的每个元素的可能性。这种所谓的“退化”情况，可能表现为每个项目是参照以前添加的项目。也就是说，只有一个子集，它的成员链像这样连接到下一个子集： a -> b -> c -> d。如果我们在 a 上调用 uf-find ，它必须枚举集合中的所有元素。

然而，有一种方法可以改进 uf-find 行为：通过压缩树的深度，使所有点沿着路径到它的根点，也就是说，将每个链压缩成深度为 1 的宽浅型的树。

d^ ^ ^| | |a b c

不幸的是，对于整个子集，我们不能立即这样做，但是，在每次 uf-find 运行期间，我们可以压缩一条路径，这也会缩短子树中植根于其上的点的所有路径！尽管如此，这还不能保证不会有足够多的结合序列，使树长得比发现的树还要快，能把树“压扁”。但是还有另一个调整，结合了路径压缩，可以确保两个操作的次线性（sublinear）（实际上，几乎是恒定的）时间：跟踪所有树的大小，并将较小的树链接到较大的树下面。浙江确保所有的树的高度都低于 (log n) 。严格证明这一点是相当复杂的，尽管如此，但凭直觉来看，我们可以通过观察基本情况看出这种趋势。如果我们加上二元树和一元树，我们仍然会得到高度为 2 的树。

下面是优化版本的实现代码：

(defstruct pointparent(size 1))(defun uf-find (point)(let ((parent (point-parent point)))(if parent;; here, we use the fact that the assignment will also return;; the value to perform both path compression and find(:= (point-parent point) (uf-find parent))point)))(defun uf-union (point1 point2)(with ((root1 (uf-find point1))(root2 (uf-find point2))(major minor (if (> (point-size root1)(point-size root2))(values root1 root2)(values root2 root1))))(:+ (point-size major) (point-size minor))(:= (point-parent minor) major)))

在这里，Lisp 的多个值很方便，可以简化代码。有关它们的更多细节，请参见脚注 [1]。

所提出的方法在实现上相当简单，但在复杂性分析上却很复杂。因此，我只能给出最后的结果：m 并查集操作，使用树加权和路径压缩，在一组 n 个对象执行 O((m + n) log* n) （其中， log* 是迭代对数：一个增长非常缓慢的函数，在实际应用上，可以被认为是一个常数）。

最后，如果 O(n) 中几乎所有的点都不属于同一子集（其中 n 是要检查的点的数量 [2]，所以 O(1) 就是两个点），这种情况该如何检查呢？请看以下示例代码：

(defun uf-disjoint (points)"Return true if all of the POINTS belong to different subsets."(let (roots)(dolist (point points)(let ((root (uf-find point)))(when (member root roots)(return-from uf-disjoint nil))(push root roots))))t)

从这个简单的例子中可以得出更多的结论：

1. 我们最初的想法并不总是完美无缺的。检查边缘情况是否存在潜在问题是很重要的。

2. 我们已经目睹了一个压根就不存在的数据结构示例：信息片段分布在各个数据点上。有时，可以选择以集中的方式将信息存储在专用结构（如哈希表之类）中，或者将其分布存储在各个节点上。后一种方法通常更优雅，也更有效，尽管它并不是那么明显。

脚注：

[1] 此外，Python 有专门的语法来析构这类元组：dec, rem = truncate(3.14)。但是，这并不是处理从函数返回一次值和一个或多个二次值的最佳方法。所有必需的值都是通过 value 表单返回：(values dec rem) ，可以用 (multiple-value-bind (dec rem) (truncate 3.14) ...) 或 (with ((dec rem (truncate 3.14))) ...) 来检索。它更优雅，因为可以通过通常方式调用函数来随意丢弃二次值：(+ 1 (truncate 3.14)) => 4：在 Python 中是不可能的，因为你不能用某个东西对元组进行求和。

[2] 实际上，这里的复杂度是 O(n^2)，这是由于使用了在 O(n) 中执行集合成员测试的函数 member，但这对整个概念来说并不重要。如果期望使用数十个或数百个点调用 uf-disjoint，那么跟结构必须更改为具有 O(1) 成员操作的哈希集。

作者介绍：

Vsevolod Dyomkin，Lisp 程序员，居住在乌克兰基辅。精通乌克兰语、俄语和英语。目前正在撰写关于 Lisp 的书籍 Programming Algorithms in Lisp，该书将使用 CC BY-NC-ND 许可（创作公用许可协议），供公众免费阅读。

原文链接：

LISP, THE UNIVERSE AND EVERYTHING